离散数学(下)概述
10 图
10.1 图的分类
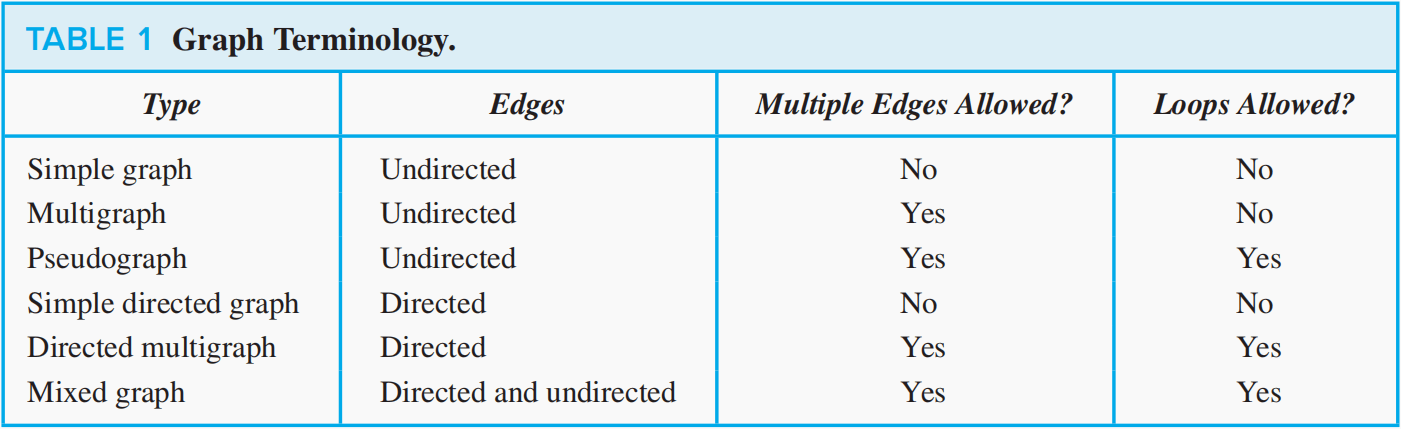
* 第三行的Pseudograph直译为伪图。
10.2 图的术语和一些特殊的图
10.2.2 一些术语
-
定义1 adjacent(相邻):一条边(edge)上的两个顶点(vertex,复数为vertices)是相邻的;这条边与顶点关联(incident)
-
定义2 neighborhood(邻居):
对于图
, - 对一个顶点
,它的邻居 = { } - 对一个集合
, 是 的子集,则 ,即A中所有顶点的邻居的并集
- 对一个顶点
-
定义3 degree(度):对无向图的一个顶点
,它的度 与其关联的边数。特别地, 上的环(loop)一个顶俩(计两次数,可以理解为一条边的两头都是 ,关联两次)。 - isolated(孤立的):指度为0的顶点
- pendant(悬挂的):指度为1的顶点
-
定理1 handshaking theorem(握手定理):
条边的无向图,有 ,也即所有顶点的度之和是边数的两倍。注意即使有多条边和环时依然成立。 这是因为一条边与两个顶点关联,就会使它们的度增加2,于是
条边总共能使顶点有 的度。 -
定理2 一个无向图有偶数个度为奇数的顶点。
比较显然,由握手定理,所有顶点度之和为偶数
,度为偶数的顶点的度之和一定是偶数,因此度为奇数的顶点的度之和也是偶数,因此必有偶数个。 -
定义4
是一条有向边,则称 邻接到(adjacent to) ,或 从 邻接 (adjacent from), 称为这条边的起点(initial vertex), 称为终点(terminal vertex)。环具有相同的起点和终点。 -
定义5
- 一个顶点
的入度(in-degree),记作 ,就是所有 作为终点的边的个数(被其他顶点指向的次数) - 一个顶点
的出度(out-degree),记作 ,就是所有 作为起点的边的个数(指向其他顶点的次数) - 一个环使顶点的出度和入度同时+1
- 一个顶点
-
定理3 对存在有向边的图
,有 ,即 总出度=总入度=边总数 考虑到一条边一定对应一出一入,比较显然。
-
概念:忽略一个图的有向边的方向,所构成的无向图称为基本无向图(underlying undirected graph),一个图与它的基本无向图有相同的边数。
10.2.3 一些特殊的图
-
Complete Graphs(完全图)
一个简单图,任意两个顶点之间都有且仅有一条边,即为完全图
n个顶点的完全图是确定的,记作
有 
相对地,如果一个简单图至少有一对顶点之间没有边,则它是不完全的 (noncomplete)
-
Cycles(环图)
n个顶点的图,
, 若包括顶点
和边 ,则称为环,记作 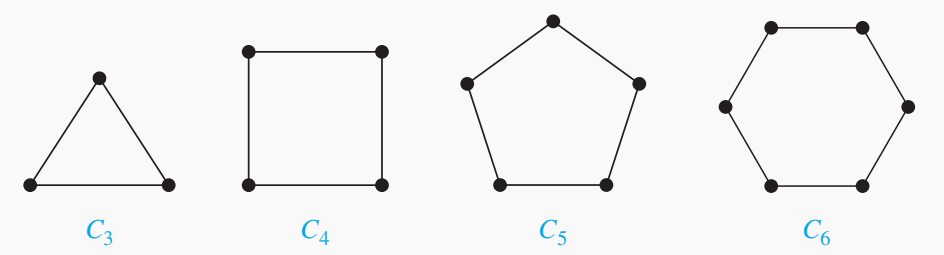
-
Wheels(轮图)
给n顶点的环(
)再加一个顶点,然后把这个新顶点与其它所有顶点用一条边连接,就形成了轮,记作 ,需要注意 只有n-1个顶点。 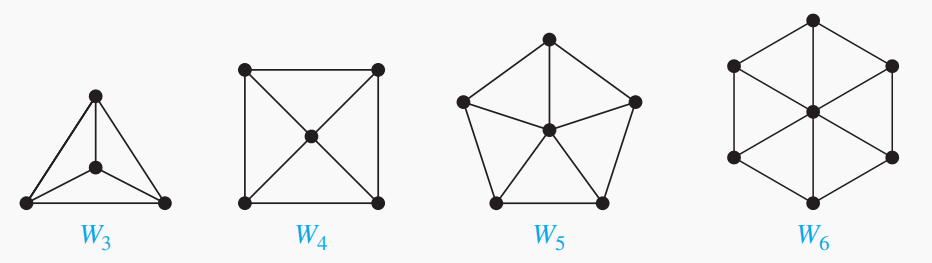
-
n-Cubes(n维超立方体)
一个n-cube有
个顶点,用长度为n的二进制串给它们编号,任意两个编号恰有一位不同的顶点相邻,记作 。 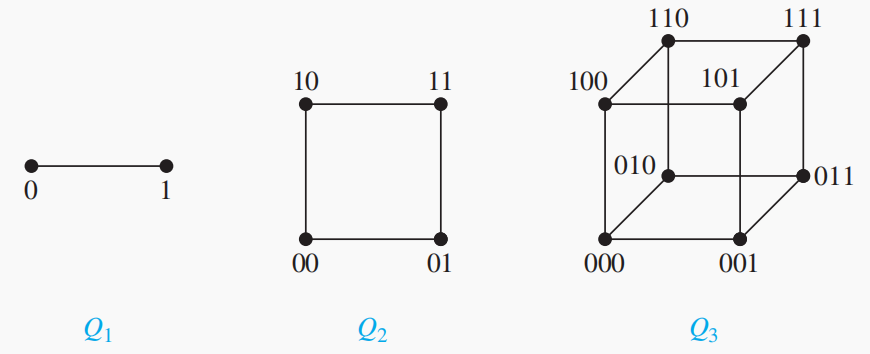
10.2.4 二分图(Bipartite Graphs)
-
定义6 bipartite graph(二分图):对于一个简单图
,如果它的顶点集合 能够被划分成两个不相交的子集 和 ,使得图中的每条边都连接一个 中的顶点和一个 中的顶点(因此 或 内部没有边),我们称 是二分的(bipartite), 是 的顶点集 的一个划分(bipartition)。 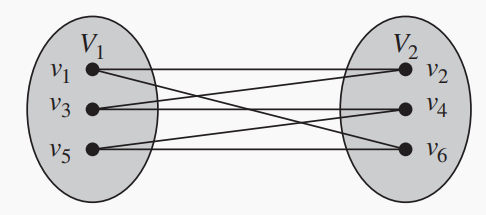
-
定理4 一个简单图是二分的,当且仅当你可以用两种不同的颜色涂满所有顶点,保证没有两个相邻的顶点被涂上同一种颜色。
显然,将两种颜色的顶点分别归于两个集合,那么这两个集合就是一个划分。
-
概念:设一个图上有一个划分
, 和 中分别有 m 和 n 个顶点,且 和 中的任意两个顶点之间都有边(都是相邻的),那么这个图是完全二分图(Complete Bipartite Graphs),记作 
10.2.5 图的转换(New Graphs from Old)
-
定义7 subgraph(子图):一个图
的子图是一个图 ,满足 且 。如果 ,那么 是 的真子图(proper subgraph)。 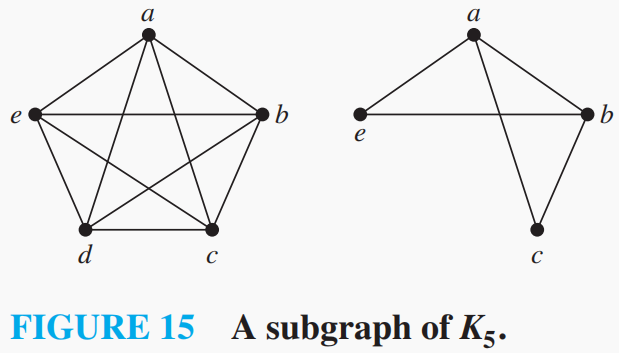
-
定义8 subgraph induced(导出子图):由一个图的顶点集合的一个子集,和两端顶点均在这个子集中的所有边的集合组成的图,称作由这个子集导出的子图。
相当于从一个图中抽出几个顶点,保留它们原本的边,这个新的图就是这些顶点导出的子图。
如下图所示,取
,则 的导出子图为右图所示 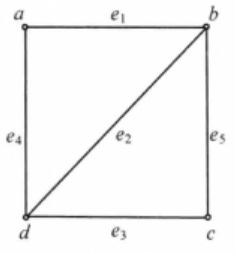
-
定义9 union(并图):设
, ,则 称为 和 的并图 (union),记为 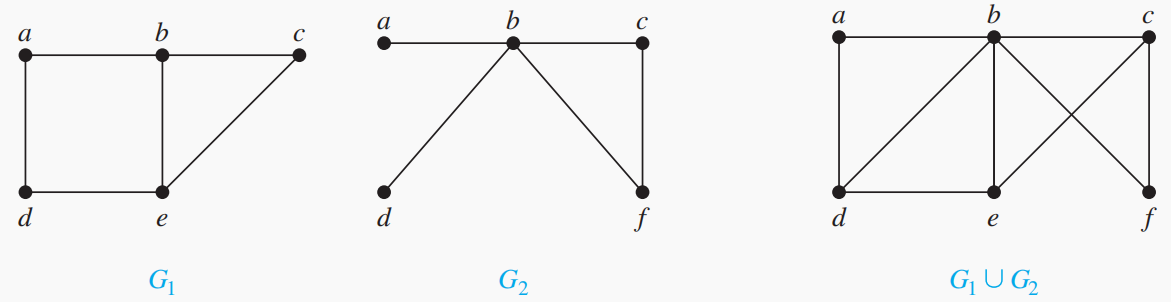
-
定义(补充) Complementary Graph 补图(绝对补图):
的补图即完全图 去除 的边集后得到的图 ,记作 。 也即 与 的边是互补的。 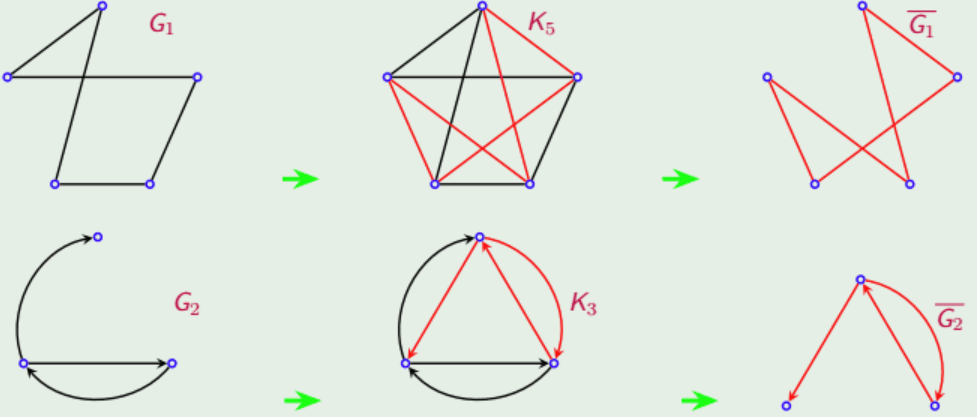
-
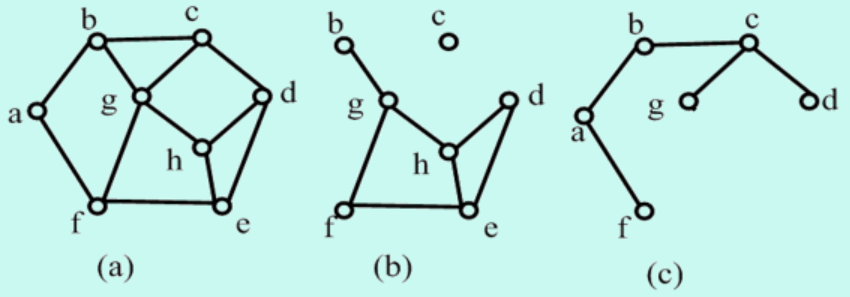
定义(补充) 相对补图:设
, 为其子图,则 称为 相对于 的补图,其中 为 中的边所关联的所有顶点的集合。(也就是说补图中不存在孤立点,因为没有一条边与它关联)
10.3 图的表示与图的同构(Representing Graphs and Graph Isomorphism)
10.3.1 Introduction
有许多方式可以表示一张图,我们需要讨论几种图的表示方法。
有时两张图有完全相同的形式,意思是它们保留了边的顶点能够建立起一一对应的关系,于是我们称它们是同构(isomorphic)的,判断两张图是否同构是图论中的一个重要问题。
10.3.2 图的表示(Representing Graphs)
-
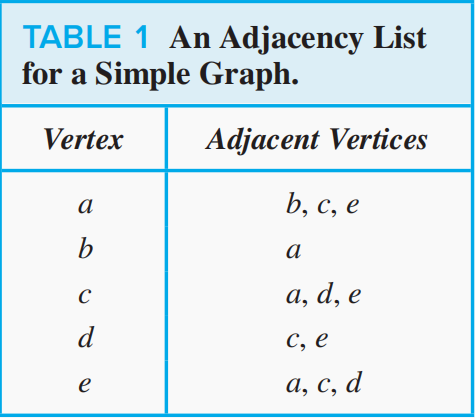
概念:可以依次列出每个顶点的相邻顶点来表示一张图,这张表叫做 adjacency lists(邻接表),如果是有向图,可以列出所有起点的终点。

10.3.3 邻接矩阵(Adjacency Matrices)
-
概念:给一个简单图
的 个顶点编号,列为 ,则 G 的 adjacency matrix(邻接矩阵) (或记作 )是一个 的矩阵,当且仅当 和 相邻, ,否则 。 也即
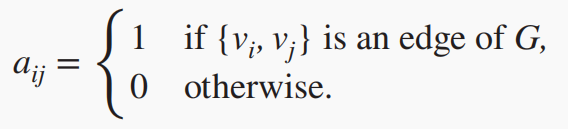
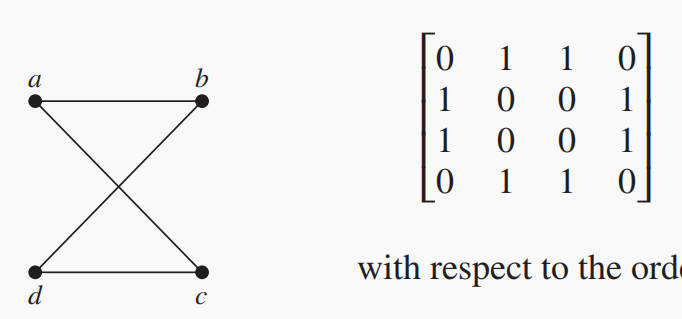
而对于多重无向图,将
拓展为 之间的边数,得到的 就是其邻接矩阵。 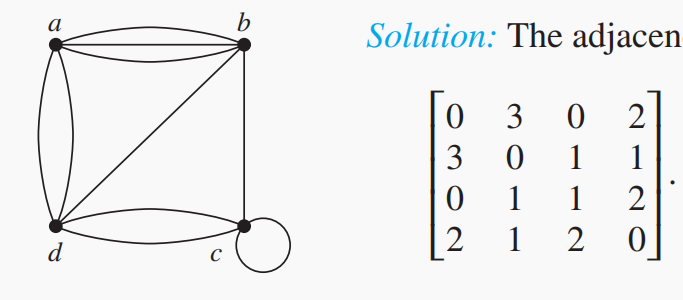
值得注意的是,对于无向图,其邻接矩阵一定是对称的(两个相邻的顶点是对称的)
于是可以拓展出有向图的邻接矩阵,只要令
是 的边数即可(也就是以 为起点, 为终点的边数) -
拓展:邻接表和邻接矩阵之间的权衡(TRADE-OFFS BETWEEN ADJACENCY LISTS AND ADJACENCY MATRICES)
如果一张简单图的边数相对较少,也即称之为稀疏的(sparse),那么通常更加适合使用邻接表来表示。如果用邻接矩阵表示的图是一张稀疏图,我们称它是一个稀疏矩阵(sparse matrix),它的非零元素较少,我们有一些特别的方法来记录和计算它。
现在考虑一张稠密的(dense)图,它则更适合使用邻接矩阵来表示,因为当我们需要知道
是否是图的边时,使用矩阵只需要看 是否为1,而使用表需要依次查找与 相邻的顶点,看其中有没有 。 总结:稀疏图用表,稠密图用矩阵
10.3.4 关联矩阵(Incidence Matrices)
-
概念:设无向图
,它有 个顶点 和 条边 ,则其incidence matrices(关联矩阵)为 ,满足 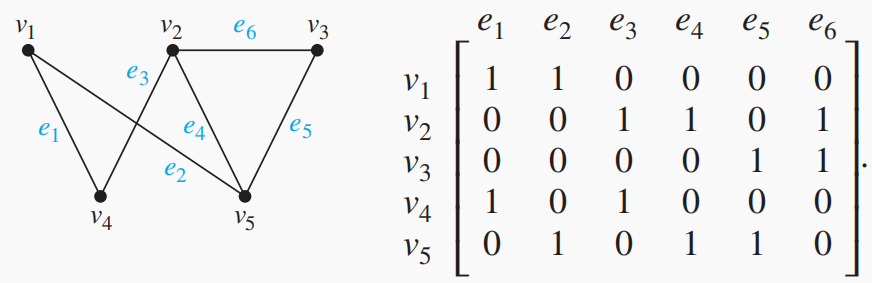
关联矩阵可以用来表示带环(loop)的多重图,值得注意的是用来表示环的一列有且仅有一个元素为1(因为只有一个顶点与环关联),但通常情况下一列有两个元素为1,因为通常一条边与两个顶点相关

10.3.5 图的同构(Isomorphism of Graphs)
-
定义1 对于两张简单图
和 ,如果存在一个 一一对应的(双射的)函数 ,满足 和 在 中相邻,当且仅当 和 在 中相邻,我们称这两张图是同构的(isomorphic),而函数 是一个同构(isomorphism),两张不同构的简单图被称作是 nonisomorphic 换句话说,同构就是一个保留了相邻关系的顶点的一一对应关系。
-
拓展 有向图的同构与简单图类似,但是顶点的映射需要保留原本的方向关系,也就是说,
需要满足在 中 邻接到 ,当且仅当在 中 邻接到
10.3.6 确定两张简单图是否同构
-
概念 确定两张图是同构的比较困难,因为我们需要确定所有的一一对应的顶点都保留了边的关系,但是确定两张图是不同构的则相对简单。一些属性在图的同构中会被保留,我们称其为graph invariant(图形不变量),比如顶点数、边数和后续提到的连通性、回路存在性等,如果这些量发生改变,我们很容易知道两张图是不同构的。
每个顶点对应的度就是一个图形不变量,如果两张图的顶点的度不能形成一一对应关系,那么可以判断它们不同构。
可以通过画邻接矩阵来判断两张图是否同构,如果一个矩阵能够通过行或列的交换变成另一个矩阵,那么就可以说明它们是同构的,通过比较其行列序号也可以找到对应的
需要注意的是如果一个
是一个同构,我们可以得知两张图同构,但 不是一个同构不能推出两张图不同构,因为其它 可能是一个同构。
10.4 连通性(Connectivity)
10.4.1 Introduction
许多问题都可以被建模成一条由图的边构成的路径。比如两点是否能够连通,或者寻找最优路径等,这时就可以用到图的路径模型。
10.4.2 路径(Paths)
通俗来讲,路径就是一系列的边,从一个顶点开始,沿着边经过一个又一个顶点。
-
定义1
设
, 是无向图,将 中从 到 的 个的顶点序列 的 条边 称为 G 的从 到 的长度为 的路径 (path),其中对于 , 连接 和 - 称以上定义的路径经过(pass through)顶点
或遍历(traverse)边 - 当该图是简单图时,可以用顶点序列
表示该路径 - 若
且 ,即该路径在相同的顶点开始和结束,则称它是回路(circuit) - 若路径或回路不包含相同的边,则称它是 简单的(simple)
- 称以上定义的路径经过(pass through)顶点
-
定义2
对有向图来说,它从
到 的长为 的路径是图中的一系列与 关联的边 ,其中 ,满足前一条边的终点是后一条边的起点。如果没有多重边,路径可以记作 ,其余定义与无向图类似。
10.4.3 无向图中的连通(Connectedness)
-
定义3 connected(连通的):如果一个无向图中的每一对不同的顶点之间都有一条路径,那么我们称它是连通的。否则称之为不连通的(disconnected)。我们说我们分割(disconnect)一个图,当我们通过移除顶点或边的方式来产生一个不连通的子图。
简单来讲,连通就是指图中任意两顶点之间都有路径。
-
定理1 一个连通图中的任意两不同顶点间都一定有一条简单的路径(不走回头路)

简单讲:由于是连通图,任意两点间一定有一条最短路径。假如这条路径不是简单的,也即路径中有两条重复的边,那么一定有两次来到同一个顶点,把这中间的路径删除可以得到一条更短的路径,于是就矛盾了。
-
概念:一张图的connected component(连通分量)是指它的极大连通子图(不是其它连通子图的真子图)。一张不连通的图
至少有两个或以上的连通分量,满足互不相交且它们的并图是 。 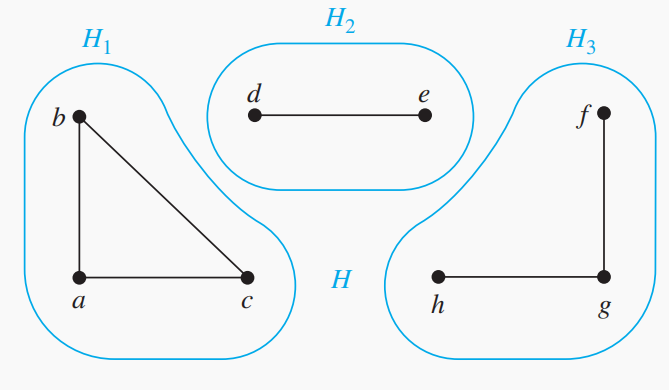
10.4.4 一张图是如何连通的?(How Connected is a Graph?)
一些概念
-
如果我们删除图中的某些点及与其关联的边,产生的子图具有比原来更多的连通分量,那么称之为cut vertices/articulation points(割点/关节点)。从一个连通图上删除一个割点会产生一个不连通的子图。
类似地,具有这样性质的边被称为cut edge/bridge(割边/桥)。
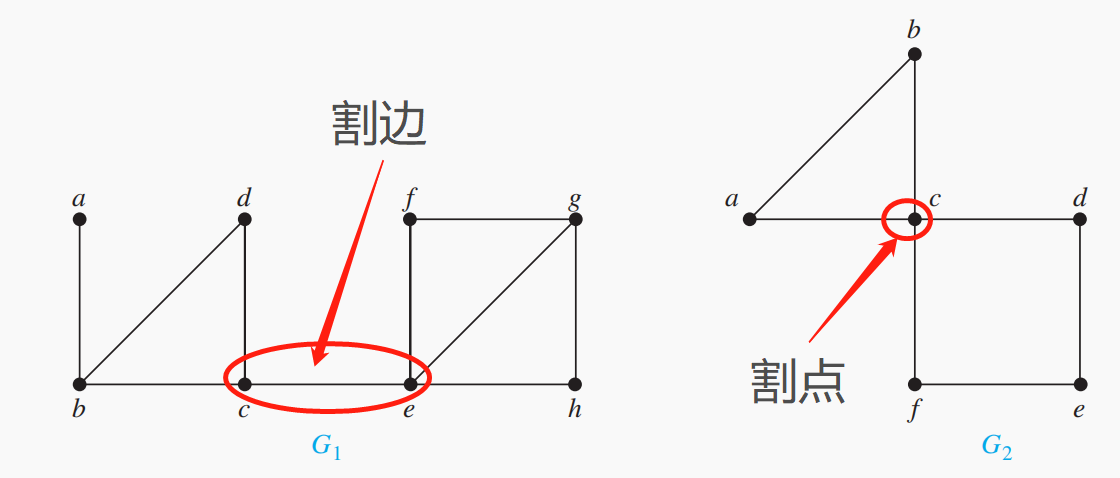
-
不是所有的图都有割点,比如
,删去任意一个顶点只会变成 ,我们称没有割点的连通图为nonseparable graphs(不可分图)。可以认为它们比那些有割点的图连通性更强,进一步,我们可以考虑用一张图能被分割需要的最少的顶点数来衡量它的连通性。 -
如果一张连通图删去某些点(包括相关的边)之后变成了不连通的,我们称这些点组成的集合为vertex cut/separating set(点割集)
-
定义非完全图
的vertex connectivity(点连通性)是一个点割集中最少的顶点数量,记作 由于
删去任意顶点之后还是完全图(于是也是连通的),因此完全图没有点割集。我们规定 ,也就是把 变成一个单顶点图需要删除的顶点数。 -
如果
, 称图 为 -connected ( 连通的)。 1连通的图是一个非单顶点的连通图,2连通的图(称作biconnected)是不可分的(没有割点)且至少有三个顶点。注意一个
连通的图也是 连通的图。 -
类似点割集,可以定义 edge cut(边割集)和 edge connectivity(边连通性)。边连通性也即边割集可含的最少的边数,记作
,对任意包含多于一顶点的图,这个定义都成立,因为把与一个点相关的全部边删光总能得到一个不连通的子图。 -
-
关于点连通性和边连通性有以下不等式
对于后半部分,可以考虑与度最小的顶点关联的边一定是一个边割集。
对于前半部分,可以考虑对于最小的边割集,其每条边上任取一端点组成的顶点集一定是点割集,这样取出的端点个数一定小于等于边的个数(可能一个顶点对应多条边)
10.4.5 有向图的连通
-
定义4 strongly connected(强连通的):如果一个有向图的任意两个顶点
之间都同时有一条从 到 的路径和一条从 到 的路径,那么称这个图是强连通的。 -
定义5 weakly connected(弱连通的):如果一个有向图的基本无向图(删去所有边的方向)中的每一对顶点之间都有路径,则称该图是弱连通的。
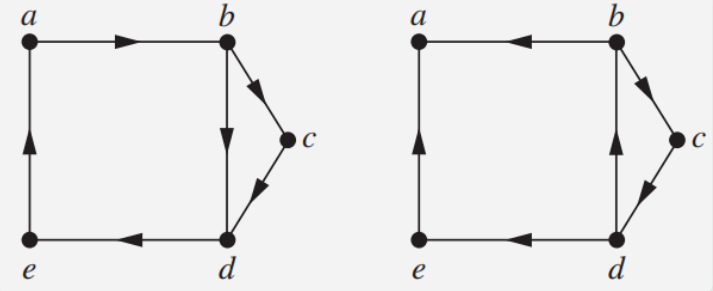
左图是强连通的,右图是弱连通的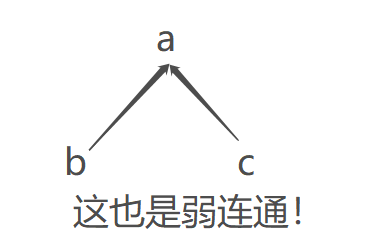
-
概念:一张有向图的极大强连通子图 (不是任何强连通子图的真子图) 称为它的强连通分量(strongly connected components)或简称为强分量(strong components),
需要注意的是一张有向图的两个顶点所在的强分量要么相同,要么互不相交。
如果两个顶点连通,那么相同,反之互不相交
10.4.6 路径与同构(Paths and Isomorphism)
我们有时可以通过路径和回路来判断两张图是否同构。比如特定长度的简单回路的存在是一个有用的不变量。除此之外,路径可以用来构造可能是同构的映射。
10.4.7 路径的计数(Counting Paths Between Vertices)
一个图中两个顶点间的路径数量可以用它的邻接矩阵来确定
-
定理2 一张图(有向边或无向边均可,允许多重边和环路)的以
的顺序排列的邻接矩阵为A,则从 到 的长为 的不同路径的数量为 的元素 类似二元关系中的传递概念,数学归纳法易证。
-
概念:
个顶点的图 中, 是 的邻接矩阵,则 称为 的可达性矩阵。 可达性矩阵反应了图的某些性质:
对于有向图:
(1)
中元素全为1 当且仅当 是强连通的(可以对应传递闭包,比较好理解) (2)
的可达性矩阵元素全为1 当且仅当 是弱连通的(也就是消除了边的方向性) 对于无向图:
中元素全为1 当且仅当 是连通的(有向图的弱化版本,无向图中 ,也不用考虑强连通还是弱连通)
10.5 欧拉与哈密顿路径(Euler and Hamilton Paths)
10.5.1 Introduction
我们能否从一个顶点开始,遍历每一条边(不重复)之后回到这个顶点?相似地,我们能否遍历每一个顶点(不重复)之后回到这个顶点?前面的问题所描述的路径就是欧拉回路(Euler circuit),而后者则是哈密顿回路(Hamilton circuit),两者看起来很相似,但是第一个问题可以通过相对简单的,检查顶点的度的方法来确定;而第二个问题则困难许多。
10.5.2 欧拉路径和回路(Euler Paths and Circuits)
-
定义1 Euler circuit(欧拉回路):图
中的一个欧拉回路就是一个包含了 的每条边的简单回路。 的一个欧拉路径(Euler path)就是一个包含了 的每条边的简单路径。有欧拉回路的图被称作欧拉图(Euler graph)。 (10.4.2)若路径或回路不包含相同的边,则称它是 简单的(simple)
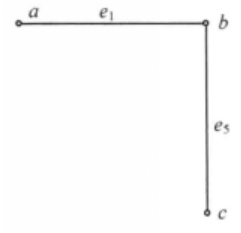
需要注意的是对于有向图,边的方向也是需要考虑的,比如下图就没有欧拉回路或路径
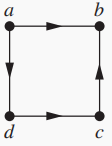
-
定理1 一个至少有两个顶点的连通的多重无向图有一个欧拉回路当且仅当它的每个顶点的度都是偶数。
先证明充分性,即存在欧拉回路的图,它的每个顶点的度都是偶数:
一种理解是,可以按照顺序把欧拉回路的边列出来,比如
,可以看到由于欧拉回路的性质,每条边都互不相同,而且每条边的顶点都首尾相接(最后的终点与最初的起点相同),也即每个顶点如果在一条边中出现一次,那么一定会在另一条不同的边中再出现一次,于是每个顶点都一定与偶数条边关联(环例外,但与后面的结论不冲突),因此每个顶点的度都是偶数的;更更直观的理解是,以一个顶点为起点,沿着欧拉回路走一圈,每进入一个顶点就要走出一个顶点,这样一次一个顶点的度加2,最后走回起点,起点一出一如度也为2,于是得证。 其次证明必要性,也即证明如果连通图中所有的顶点的度都是偶数,那么必然存在一个欧拉回路。这个证明相对困难,我们采用构造性证明的方法:
首先我们需要证明这样的图中一定可以找到一个简单回路。
我们任取图中一顶点作为起点,走到任意一个与它相邻的顶点(这是肯定可以做到的,因为顶点数量
且是连通图),再找一个与这个点相邻的顶点,走过任意一条之前没走过的与该顶点关联的路径,不停重复这一步,直到走到一个顶点,它的任何关联路径都是之前走过的,于是操作结束。首先由于这是一个有穷图(默认),它有有限条边,而每次操作都会走过一条之前没走过的边,因此上述操作一定是可行而且可以结束的,于是我们确定它是一条简单路径(一路上没有重复的边);不仅如此,我们可以证明它的终点一定就是起点。因为这个图的所有顶点的度都是偶数(至少为2),所以不可能停在除起点之外的顶点,否则可以反证,若停在某个顶点,如果之前没经过这个顶点,那么与这个顶点关联的边只有一条(来的这条),与度为偶数矛盾。而如果之前经过了这个顶点,每次一进一出就有两条不同的关联边,这次进来是走的最后一条关联边,那么总共还是奇数条边,依然矛盾。综上,这是一个简单路径,其起点又等于终点,因此它是一个简单回路。 接下来我们来构造这张图的欧拉回路。
有了上述证明的保证,我们首先在一个所有顶点的度都是偶数的连通的多重无向图
中任意找一个简单回路。用这个简单回路经过的边及其端点构成一张 的子图,那么显然这个子图是一张欧拉图,这个简单回路是这张子图的欧拉回路,而根据之前充分性的证明(存在欧拉回路的图,其每个顶点的度都是偶数),这个子图中所有顶点的度都是偶数。这说明简单回路中所有顶点关联的边数都为偶数。 现在从
中删除这个回路中所有的边。 如果回路剩下的全部都是孤立点,而 中没有其它边了,因为 中本来不可能有孤立点(它是连通的),那么说明这个回路中的边包含了 中所有的边,那么这个回路就是一个欧拉回路,构造完毕。 如果回路剩下的全部都是孤立点,而 中还有其它边,那么说明 中有一些顶点,与回路中的任意顶点之间不存在路径,那么违反了 的连通性,是不可能的。因此回路一定会剩下某些顶点,其关联了 条在 中但不在回路中的边。由于 中任意顶点的度为偶数,而回路中任意顶点在回路中也与偶数条边关联,因此 一定还是一个偶数。我们任选一个这样的顶点作为起点,重复之前构造简单回路的方法,沿着某条不在回路中的边,继续构造一个新的,与之前回路中的边不重复的简单回路。接着,以这个公共顶点为起点,走通新的回路,找寻回路,连接两个简单回路形成一个新的回路(比如这个顶点是 ,第一个回路是 ,第二个回路因为是以 为起点的,设为 ,那么合成之后变成 ),这仍然是一个简单回路,于是再删除这个回路中的边。。。不停重复上述操作,由于每次构造新的简单回路都要用到之前没用过的边,而 的边是有限的,因此总能回到情况 ,于是就构造出了一个欧拉回路。 -
拓展:Fleury’s algorithm(弗罗莱算法)
我们可以用弗罗莱算法求一张欧拉图的欧拉回路,其过程如下:
-
设图为
,从图中任取一顶点 ,令路径 ; -
假设沿
走到顶点 ,按下面原则从 : -
与 相关联; -
除非没有别的边可供选择(此时可以任选一条),
不是 中的桥。 (10.4.4)桥也即割边,当它被删除时会产生更多的连通分量
-
-
当 ii 不能进行时算法停止。
可以证明,当算法停止时,得到的简单回路
是 中一条欧拉回路。 简单讲,就是每次走到一个新的顶点,就选一条之前没走过的边继续走,而且尽量不走割边。
可以朴素地理解为,尽量不走割边,就不会破坏图的连通性,于是就可以走完图中的每一条边。
-
-
定理2 一个连通的多重图有一个欧拉路径(但不存在一个欧拉回路)当且仅当它恰有两个顶点的度为奇数。
和欧拉回路类似。区别就是,一个起点和一个终点,前者某次只出不进,后者某次只进不出,它们的度都是奇数,其余顶点的度为偶数。
应用这个定理我们可以判断一笔画问题有没有有解;如果有解的话,任取一个度为奇数的点作为起点,然后尽量不走割边即可。
-
定理(拓展)
-
含有至少2个顶点的有向多重图具有欧拉回路当且仅当它是弱连通(这里说强连通也是等价的,因为弱连通且满足后面条件的有向图一定是强连通)的,且每个顶点的入度等于出度。
和无向图的证明类似。
-
含有至少2个顶点的有向图具有欧拉路径当且仅当该图是连通的,且恰好含有两个顶点,一个入度比出度大1,一个入度比出度小1,其余顶点的入度等于出度。
和无向图的证明类似。
-
10.5.3 哈密顿路径和回路(Hamilton Paths and Circuits)
-
定义2 图
中一条恰好经过所有顶点一次的简单路径被称为哈密顿路径(Hamilton path),而 中一个恰经过每个顶点一次的简单回路被称为哈密顿回路(Hamilton circuit),简称H回路。存在哈密顿回路的图被称为哈密顿图。 哈密顿回路还可以被定义成一个首尾相接的哈密顿路径。
-
定理(拓展):
一定有哈密顿回路。 实际上,
就一定有哈密顿回路。 (10.2.3)
即 个顶点的完全图, 即 个顶点的环。 -
拓展:哈密顿回路存在的条件
与欧拉回路不同,哈密顿回路的存在并没有一个简单的充要条件(尽管它们很相似)。不过,许多理论给出了哈密顿回路存在的充分条件,此外,我们可以根据图的某些属性确定一张图没有哈密顿回路。
比如,一张图中如果存在一个度为1的顶点,那么它一定没有哈密顿回路(显然它根本无法构成回路)。
一个哈密顿回路中的每个顶点都恰与回路中的两条边相关联(恰好一进一出)。
进一步地,一张图中如果有一个顶点的度为2,那么它的两条相关边必然都在哈密顿回路中(如果存在)。
又或者,如果你正在构造一条哈密顿回路,当它经过了其中某个顶点,那么除了它经过的那两条边,其余与这个顶点关联的边都可以不再考虑。
此外,一条哈密顿回路的内部不会包含一个更小的回路。否则删去小回路,由于连通性,小回路内部必然有一个顶点与外部有边关联,而这个顶点又一定和小回路内部两条边关联,因此它的关联边数大于2。这在哈密顿回路中是不可能的。
尽管目前还没有找到一个实用的哈密顿回路存在的充要条件(实际上这是一个NP难问题),但我们已知几种充分条件。记住,一张图的边越多,它存在哈密顿回路的可能性就越大;同时,给一张哈密顿图加边(而不是顶点),它仍然具有相同的哈密顿回路(参考之前提到的,可以忽略哈密顿回路之外的边)。于是我们可以不停地给一张图加边(特别是你确定加边能增加存在哈密顿回路的可能性),直到其顶点的度充分大,保证哈密顿图的存在。
下面给出一些重要的充分条件。(我们默认图是连通的)
-
定理1 Dirac’s theorem(狄拉克定理):如果
是一个有 个顶点( )的简单图,且满足 中每个顶点的度至少为 ,那么 必有一个哈密顿回路。 -
定理2 Ore’s theorem(奥勒定理):如果
是一个有 个顶点( )的简单图,且满足对于 中每一对不相邻的顶点 和 ,都有 ,那么 必有一个哈密顿回路。 -
定理(拓展) 设
(一个连通的简单图)的边数为 ,顶点数为 ,则若 ,那么 必有一个哈密顿回路。 证明:假设
是 中任意两个不相邻的顶点,把 和 及以它们为端点的边从 中删去,得到子图 ,那么 有 个顶点和 条边。因为 的边数最大为 (即任意两顶点之间都有一条边),也就是 于是
,也即 ,又由定理的条件 ,可知 ,满足奥勒定理的条件,于是得证。 -
定理(拓展) 设无向图
是哈密顿图, 是 的任意非空子集,则 ,其中 是从 中删除 (包括其中顶点及其关联的边)后的子图的连通分量的集合。 简单讲,就是删去一张哈密顿图中的某些顶点,得到的子图的连通分量数量一定比删去的顶点数量要少。可以把它作为哈密顿回路存在的必要条件。
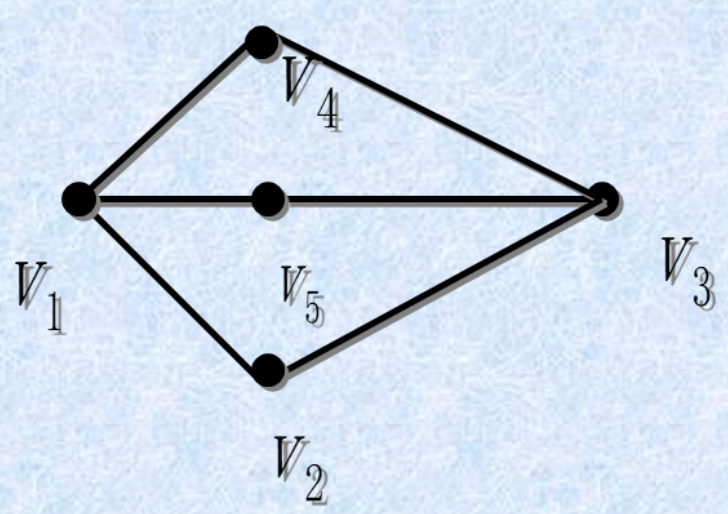
如上图,删去
和 两个顶点,剩下的图有三个连通分量,那么它不是哈密顿图。
10.5.4 哈密顿回路的应用
除了一些数据传输问题,我们讨论一下哈密顿回路在编码上的应用
-
格雷码
位的格雷码编码问题实际上就是寻找 的一条哈密顿路径。 (10.2.3)
n-Cubes(n维超立方体)
一个n-cube有
个顶点,用长度为n的二进制串给它们编号,任意两个编号恰有一位不同的顶点相邻,记作 。 
10.6 最短路径问题(Shortest-Path Problems)
10.6.1 Introduction
许多问题都可以被建模成边上带权的图。
比如下面是一张里程图
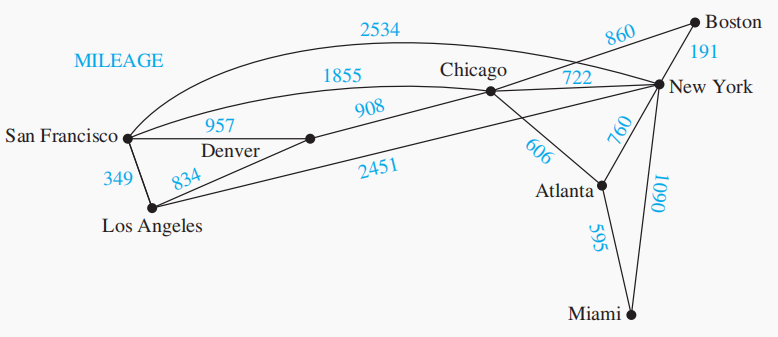
- 定义 weighted graphs(有权图):给每条边都分配了一个数(权)的图被称为有权图。
- 定义 length(长度):在一张有权图中,一条路径的长度指路径上所有边的权的和。注意这里的长度要与无权图中路径的长度,也即路径包含的边数区别。
10.6.2 一个最短路径算法(A Shortest-Path Algorithm)
对于寻找有权图中的两个顶点的最短路径问题,有几种不同的算法。我们将介绍一种由迪科斯彻发明的贪心算法(greedy algorithm)(是指一类算法),并且只介绍一个只适用于无向的,权为正数的有权图的版本。
-
定理1 迪科斯彻算法(Dijkstra’s algorithm)可以找到一个连通简单无向正权图中两个顶点间的最短路径。
简述:
- 将起点的权初始化为0,所有其它顶点初始化为
。 - 找到图中权最小的顶点
,如果这个顶点就是终点,则顶点记录的路径就是最短路径。终止。 - 考虑所有
的相邻顶点的权,如果大于 的权+两顶点之间的边的权,那么把相邻顶点的权更新为后者,并且在这个相邻顶点记录的路径的结尾加上 。 - 从图中删去
,意思是之后找顶点时不再考虑 。 - 回到步骤 ii。
可以参考下图,起点为
,终点为 。 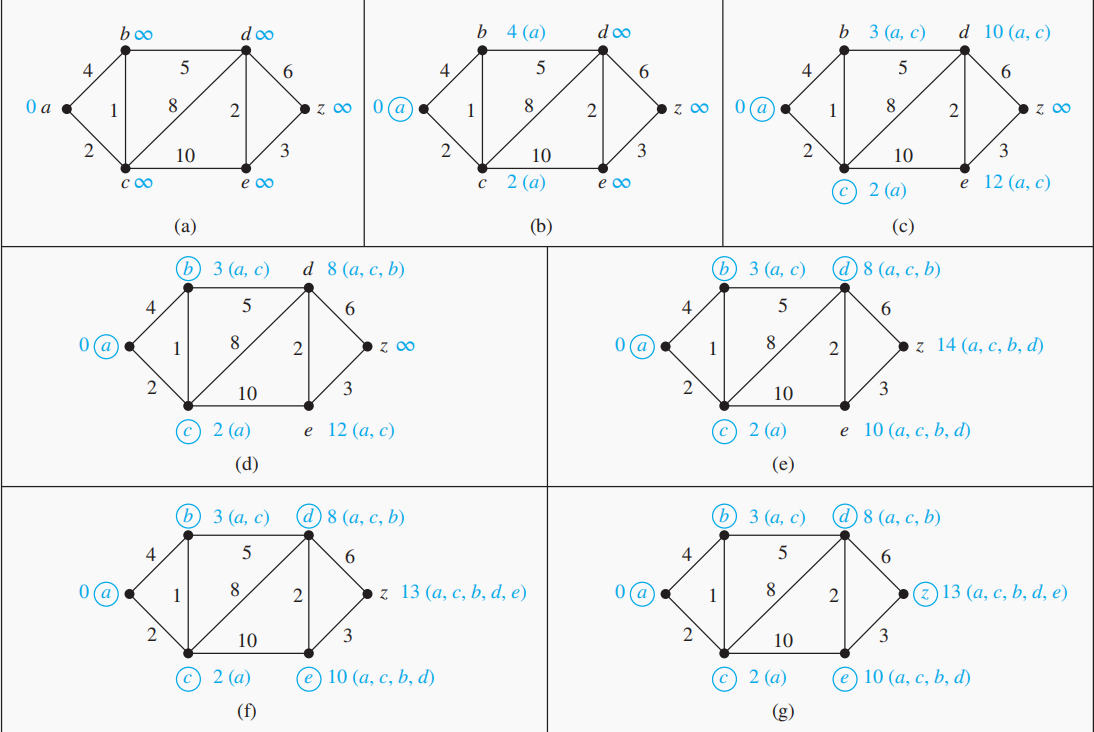
- 将起点的权初始化为0,所有其它顶点初始化为
-
定理2 迪科斯彻算法求
个顶点的图中两顶点最短路径的时间复杂度为 (在加法和比较运算上)。
(拓展)使用一次迪科斯彻算法可以计算出从某个点到其它任意点之间的最短路径,但是如果想要寻找任意两个顶点间的最短路径,我们可能需要使用
-
定义(拓展) Distance Matrix(距离矩阵):设
是一张带有 个顶点的图,它的距离矩阵是 ,它满足如下性质: 表示边 的权值 - 如果
和 之间没有边,那么 - 令
,实际上 就是从 到 的最短的两条边的路径 - 同样地,令
,实际上 就是从 到 的最短的 条边的路径
-
定义(拓展) 定义与距离矩阵相关的运算
,令 , ,则 。 那么,设
,且 ,实际上 就是从 到 的最短路径长度。
综上,我们可以通过计算距离矩阵的方式,批量求出任意两顶点的最短距离。
实际上在数据结构中会提到,这个算法就是弗洛伊德(Floyd)算法。
10.6.3 旅行商问题
有许多城市,一个旅行商想找到一条最短的路,从一个城市出发,遍历所有城市(不重复)然后回到起点,这就是旅行商问题。这是一个NP难问题。
这实际上就是求解无向完全有权图中的最短哈密顿回路的问题。
因为这是一个NP难问题,当规模较大时,目前没有算法能够在合理时间内计算出精确解,但我们可以采取一种近似算法(approximation algorithm),计算出近似的最短回路。
-
拓展:最近领域算法(nearest neighbor method)
这个算法其实很简单,就和名字一样,从一个起点开始,每次都前往距离当前顶点最近的顶点,最后再走回起点,这样就组成了一个近似的最短回路。以下是更正式的描述。
对于
个顶点的有向加权完全图的最短哈密顿回路,其求解步骤如下: - 从任意顶点
出发,取与 距离最近的顶点 ,记 为经过这两个顶点的路径。 - 如果已经记录了路径
,取不在路径中且与 距离最近的顶点 加入路径末尾。 - 重复步骤2直到
,此时将边 加入道路,则 即为所求近似解。
- 从任意顶点
这种方法的近似程度如何呢?下面是对于某类特殊的图,该算法的近似程度的描述。
- 定理(拓展) 设
是有 个顶点的完全无向图,其中 是边权的集合, 即 的权,若对于任意顶点 , 满足三角不等式 ,那么记 是最短 回路(哈密顿回路的缩写)的长度, 是最近领域法得到的近似长度,有:
10.7 平面图(Planar Graphs)
10.7.1 Introduction
考虑这样一个问题,每个房子需要连接三个电器,现在一共有三个房子,有没有一种画线的方法能保证线之间不相交呢?
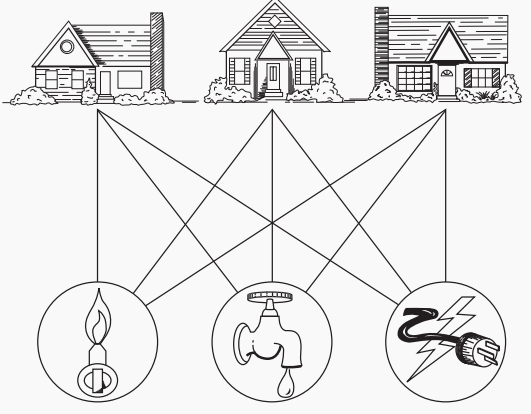
这个问题实际上可以被转换成:我们能不能在平面中,用两两不相交的边绘制出完全二分图
(10.2.4)
设一个图上有一个划分
, 和 中分别有 m 和 n 个顶点,且 和 中的任意两个顶点之间都有边(都是相邻的),那么这个图是完全二分图(Complete Bipartite Graphs),记作 
我们将在这一章学习如何确定一张图能不能在没有边交叉的情况下被画在平面上。
- 定义1 一张图被称作是平面的(planar)如果它能被画在平面上,且所有边不相交(这里的相交可以被定义为,用来表示边的线或弧相互之间存在交点,除了端点处)。这样的一种画法被称为图的一个平面表示(planar representation)。
10.7.2 欧拉公式
一张图的平面表示把平面划分成了若干的区域(regions),包括无界的区域。
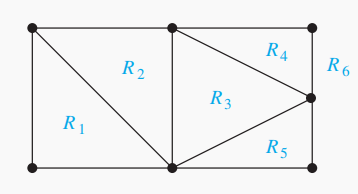
我们可以把它们称作面(face)。
-
定义(拓展) 图
的一个面是由 的边所包围的,并且其内部不含 的顶点和边的一个区域。 我们称组成一个区域
的边界回路中的边数为 的度数(degree),记作 ,需要注意如果一条边在回路中出现两次,那么它使区域的度增加 。 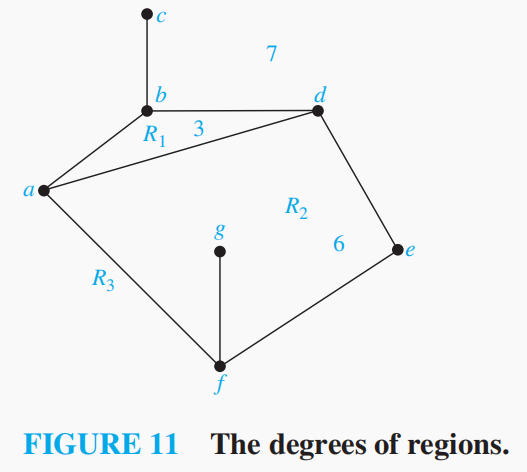
-
定理1 欧拉公式(Euler’s Formula)若
是一个连通平面简单图,有 条边和 个顶点。令 是 的一个平面表示中区域的数量,那么有 。 可以通过归纳法来证明。首先对一个图
,将其分为若干个子图 ,其中 就是从 中任取一条边(包括其端点)。在 中任意添加 中一条不在 中,且与 中顶点关联的边,就构成了 ,依此类推(因为是连通图,这个步骤总是能做到的)。 显然是满足 的 
假设
满足,那么 只有如下图两种可能 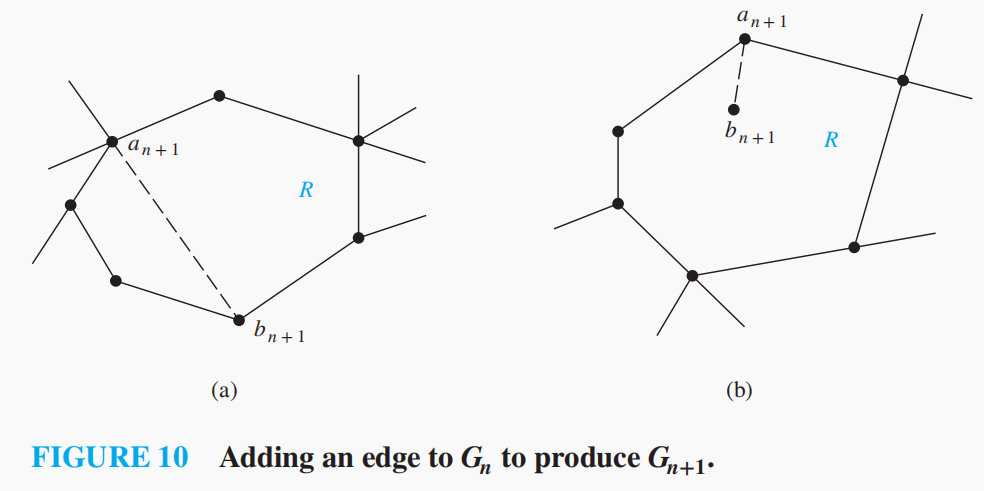
易知
同样满足 。 -
推论1 若
是一个连通平面简单图,有 条边和 个顶点,且满足 ,那么有 。 证明:对于一个简单图,因为不含多重边(可以产生度为
的区域)或者环(可以产生度为 的区域),又因为它的顶点数至少为 ,因此它的每个区域的度至少为 (包括那个无界的区域)。 我们承认以下公式
因为每条边都恰好出现在区域的边界中两次(无论是在两个不同区域中各一次还是在同一个区域中两次)。
设总共有
个区域,那么可以推出 ,又由 (欧拉公式),即可知 。 -
推论2 若
是一个连通平面简单图,那么 有一个顶点的度不超过 。 证明:如果
的顶点数为 或 ,那么推论2显然成立。否则,由推论1可知, ,即 ,由握手定理(10.2.2)知, ,若所有顶点的度都大于 ,那么就有 ,这与 矛盾,因此至少有一个顶点的度小于等于 ,证毕。 -
推论3 若一个连通平面简单图有
条边和 个顶点,满足 且没有长度为 的回路,那么有 。 证明类似推论1,只是区域的度至少为
。
10.7.3 库拉托夫斯基定理(Kuratowski’s Theorem)
我们可以知道
-
概念 简单讲,在一张图的一条边上增加一个度为
的顶点,把边一分为二(更严谨的说法是,是先删去这条边,然后增加两条与删去边的两个端点关联且同时和另一个顶点关联的边),这不改变图的平面性,我们称这样的操作为初等重分(elementary subdivision)。如果两张图可以由同一张图初等重分而成,那么我们称它们是同胚的(homeomorphic)。 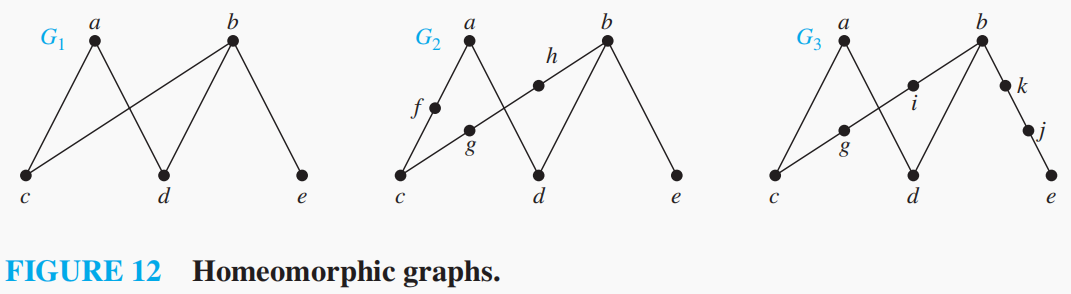
-
定理2(库拉托夫斯基定理) 一个图是非平面图当且仅当它的某个子图同胚于
或 。 充分性比较显然,但必要性的证明较为复杂,不用掌握。
10.8 图的着色(Graph Coloring)
对地图着色相关问题的研究产生了图论中的许多结论。考虑为一张地图着色(我们假定各个区域是连通的),习惯上要给相邻的不同区域画上不同颜色,我们需要知道尽可能少的能让相邻区域颜色不同的颜色数量。
比如下面的左图需要至少4种颜色,而右图需要3种。
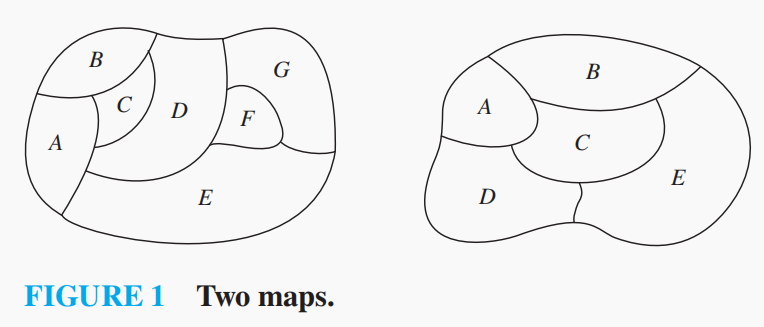
每幅地图(map)都可以被表示成一张图(graph)。
-
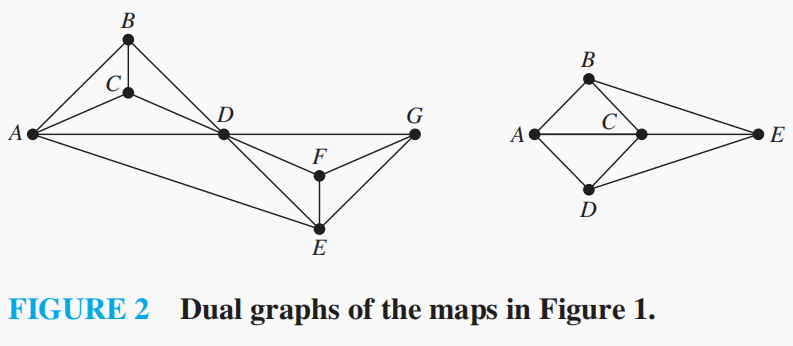
概念 我们将图中的每个区域替换成一个顶点,相邻区域对应的顶点也相邻,这样生成的图叫做地图的对偶图(dual graph)
-
定义1 一张简单图的着色(coloring)就是给每个顶点分配一个颜色,保证相邻顶点的颜色不同。
-
定义2 一张图的图色数(chromatic number)就是给这张图着色需要的最少的颜色数量。图
的图色数记作 。 -
定理1 四色定理(The Four Color Theorem): 一张平面图的图色数不超过
。 使用数学方法分类结合计算机穷举证明。纯数学的证明尚未有人完成,但五色定理的证明则容易很多。
-
一些特殊图的图色数
-
,因为任意两个顶点都相邻,因此每个顶点都需要一个颜色。 -
,给其划分的两个集合分别涂上一种颜色即可。 -
比较显然
-
-
拓展
一种着色算法
- 按照点的度数非严格递减的方式进行排序。
- 对第一个点着色,并找到与之不相邻的、在序列中与它最近的点,着相同的颜色。
- 依次类推,对序列中与已着色顶点不相邻的点按照此步骤依次进行下去。
- 删去第一次着色的点,对剩余的顶点采取步骤2的方法继续着色。
- 直到所有顶点已着色,算法结束。
该算法并不总能得到最小点着色数目。比如二分图中最小点着色是2,但是此算法可能会得到大于2的结果。
-
拓展 记使用不超过
种颜色为图 着色的方法有 个,那么 是一个多项式,称为着色多项式 。使 不为 的最小的 即为 。 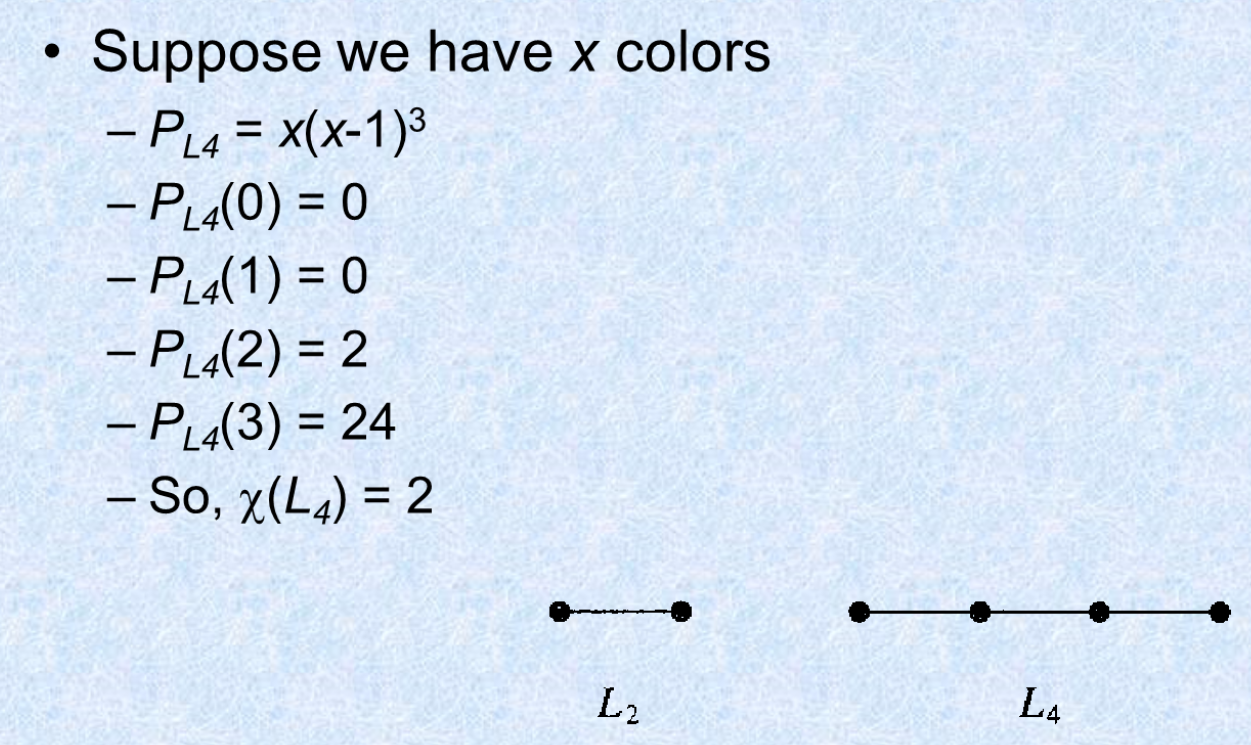
- 设
是非连通无向图,其连通分量为 ,则 - 设
是无多重边的图,设 ,记 是 删去 生成的子图, 是将 与 合并(变成一个顶点)后得到的商图,那么有
- 设