有点懒得做完整的笔记了。这个笔记将会比较轻松,简单记录自己看书时的随想随感,主要是为了增加看书的乐趣。
笔记参考张晨曦的《计算机系统结构教程(第二版)》
Chapter1
-
对广义的翻译和解释一个相当清晰的定义


-
系统结构的定义

关注软硬件的接口。指令系统的设计(机器语言所关注的)至寻址等(汇编语言关注的)都是计算机系统结构的范畴;但是主存容量与编址方式(按位、按字节或按字访问等)的确定也属于系统结构,可以说比较微妙。

可以简单地理解为,机器语言程序员编程时所需要用到的属性都在系统结构的范畴中。这个例子中,机器语言程序员编写程序时显然必须考虑到内存大小,但速度可以不考虑,因为不会影响其程序能否正常工作。
-
定量原理:
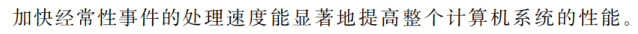
-
Amdahl
/ˈæmdɑːl/定律中的Fe与Se表示什么?不确定,也许可以理解为Fraction Enhanceable(可改进比例)和Speedup Enhanceable(部件加速比)方便记忆。
-
无聊但可能忘的公式
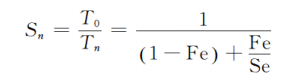
很显然不管
- 无聊但容易忘的概念

- 另一个无聊的公式
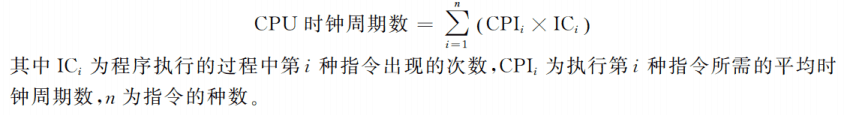
第一眼可能有点懵逼,其实就是把
-
继而得出的,超级无聊的推论

-
第九页两道例题很重要
-
局部性原理

-
执行时间和吞吐率:本质上相同,都是衡量计算机性能的指标。前者指同一个任务的执行时间,后者指单位时间执行的任务数量。
-
还记得吗?
:每秒执行百万指令数,衡量CPU性能的指标。 -
几种比较性能的平均值法比较
-
算术平均值:最简单直观的,计算平均执行时间,等价于比较执行相同程序的总用时
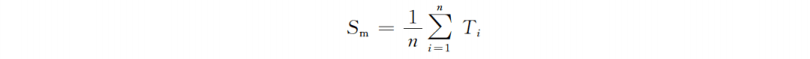
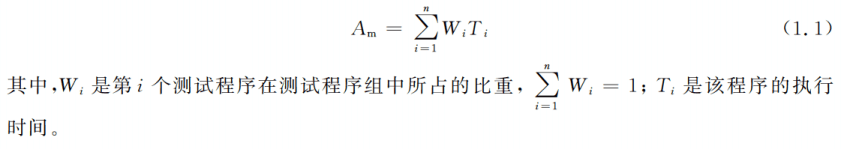
-
调和平均值:调和平均就是速度的平均,如果给出的性能数据是速度应当用这个指标。
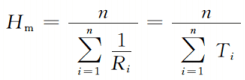
实际上观察等式最右边,可以发现和算术平均值形式是一摸一样的(因为这里的速度与时间都是以一个程序为基础,RT=1),仅仅是一个倒数的关系。这很合理,毕竟平均速度快,那平均用时就小,所以这俩平均本质上是一回事。调和平均的加权形式也就是算术平均加权取个倒数。
所以,算调和平均就用算数平均算完取个倒数即可。
-
几何平均法:下图中的
是 次根号 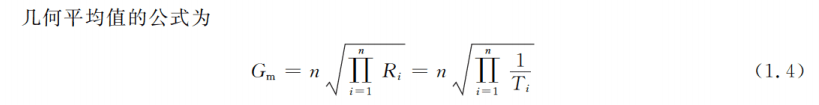
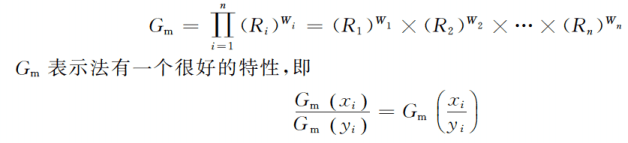
这里说的有点玄乎,我个人的理解是假设有两个计算机A、B,我们想要比较它们执行三个不同任务的性能。
-
任务1:A = 1秒,B = 4秒
-
任务2:A = 2秒,B = 2秒
-
任务3:A = 4秒,B = 1秒
显然:
- 任务1的性能比:1/4 = 0.25
- 任务2的性能比:2/2 = 1
- 任务3的性能比:4/1 = 4
不难看出,只有几何平均法能做到:平均任务性能的比(这里显然都是1) = 任务性能比的平均(这里只有几何平均是1)
-
-
-
多机系统的分类

松耦合即依靠共享外存来互联,这个例子很好想,实际上互联网可能就是一个广义的松耦合多机系统,Hadoop之类共享文件系统的集群显然也是这样。
紧耦合就不太了解了,单机多核CPU算吗?或者一些实体的服务器集群就是共享内存的?
-
可移植性的常用方法
-
统一高级语言:最高层次,不用多说。屏蔽底层实现,程序员使用完全相同的方法编程是最理想的,但现实中往往没这么理想,比如C/C++在Win和Linux上有一堆专门的库,程序员往往要自己考虑系统兼容性问题。Java是比较成功的例子。
-
系列机:系统结构层次的,或者简单讲,指令集相同(或向后兼容)
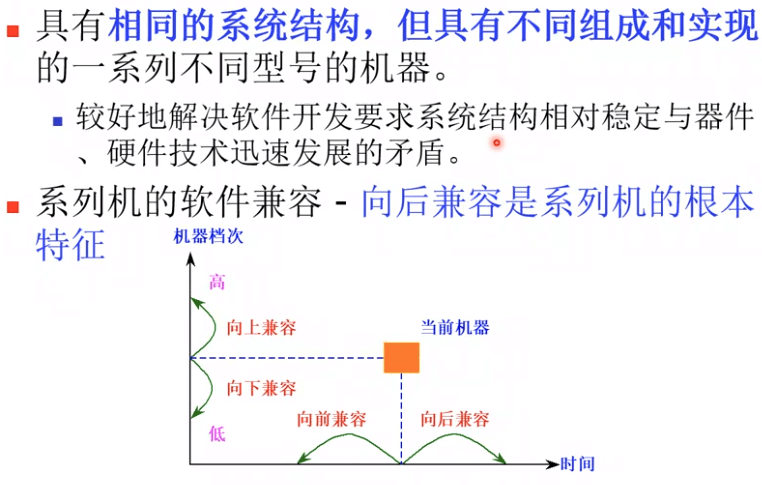
-
模拟&仿真

模拟:用软件实现另一台机器的指令集
仿真:用微程序实现另一台机器的指令集
都用解释来实现,显然仿真更底层,运行速度更快,但相应地仿真限制也更多,要求系统结构差距不大。
-
Chapter2
指令系统,教学时估计是因为计组学过所以跳过了。那这里也先跳过。
Chapter3
-
广义流水线的定义

-
排空与通过时间之间流水线才是满载的。
-
好多好多种流水线,晕晕
-
吞吐率TP(Throughput):出现过n多次的概念,对流水线来说就是单位时间流水线完成的任务数量/输出结果数量。

-
这个图咋看
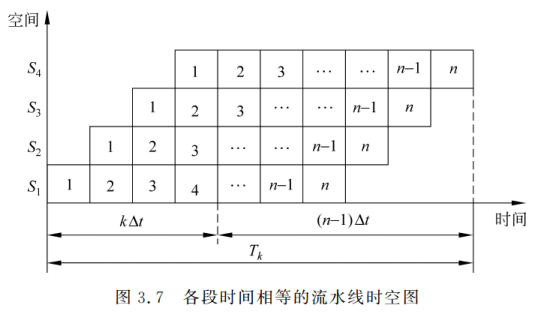
切记框框里的数字是任务号(第几个任务),空间轴坐标表明当前在处理某个任务的第几段。
如第一个
中,在处理第1个任务的第1段;第二个 中,在处理第1个任务的第2段以及第2个任务的第1段。。。以此类推。这里 是段数(这张图中就是4), 即为通过时间。 看懂了这张图,流水线的一系列公式就不难理解了。
-
公式以及一些思考

第一个公式没有太多问题,书上的解释很好(这里没截)。
第二个公式就比较有意思。首先可以看到,
似乎和 成反比,那假如任务只有一段,也就是完全串行执行任务,一个干完再干下一个, 反而可以达到最大值!流水线完全是副作用,计算机科学不存在了!想想哪里出了问题?刚刚假设的前提是, 变化的同时其它变量不变,实际上这意味着在减少任务分段的同时,不改变任务每一段的时间。。。其实也就是任务的总时间凭空变少了,这当然可以推出吞吐率变高的结论。当然实际上在任务不变的情况下,仅考虑流水线本身的优化,这当然是做不到的,因为如果我们让 减小,也就是任务分段变少,那么每一段的平均耗时 理应增加。 由此似乎还可以推出一些有趣的结论。如果我们近似认为任务分段没有时间损耗,也就是不管怎么分,加起来耗时一样,那么
就是一个定值了,于是刚刚的公式可以变形成: 也就是说,在这种假设的理想条件下,分段越多吞吐量越大,极限为n/C。
这符合直觉。实际上根据流水线时空图,想增加流水线的吞吐量,无非就是提高满载工作时间在总时间的占比。刚刚那样增加分段其实就是努力把时空图中的平行四边形努力掰成方形;而后面提到增加n提高吞吐率就是在不改变通过与排空时间的条件下,增加满载工作时间以提高其占比。
第三个公式,为什么$\lim_{x \to \infty}
TP_{MAX} \frac{1}{\Delta t}$呢? 可以这样理解:当
趋于无穷大,其通过与排空时间相对满载时间可以忽略不计,可以认为从开始到结束都是满载的,也就是每个 都完成一个任务,于是此时吞吐率即为其倒数。 -
带瓶颈的流水线
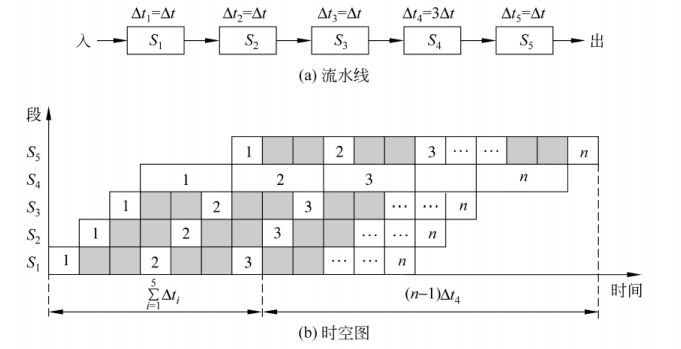
个人理解前面几段未必是要等两个
才能开始,但实际上是怎么样我也不清楚,这样安排大概是方便数据的传输,即第三段结束后数据可以立即按流水线顺序传给第四段,而不会导致冲突。 反正怎么理解也不影响TP的计算。
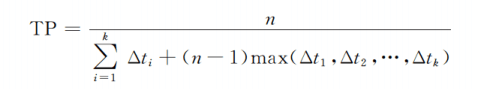

-
加速比:用流水线比顺序执行快了多少

这里其实就用到了我之前的假设,也就是顺序执行需要的时间等于所有分段之和
,其分析过程和得出的结论和我之前的联想有些类似。 -
效率
全都是一些无聊但是容易混淆的概念和公式,本质上都一样,何必分那么多?

这个结论还是比较有意思的。
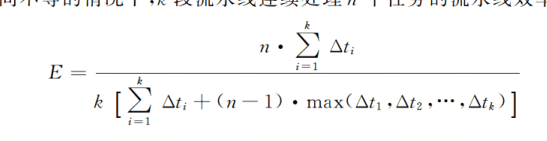
这个公式要结合上面的面积法理解,分子是n
每个任务的总时长,也就是n个任务的总时长,由于是用每段求和计算的任务时长,可以认为在计算每段时都乘上了1(这一段本身的长度),这样计算出来的其实就是所有任务的面积。分母就更好理解了,就是总时长 k段,也即时空图总面积。 亦可这样看这个公式:
这和之前教材上提出的一个推论(在各段时间相同的情况下)形式类似,只是把
换成了平均每段时间。 
这个公式怎么从意义上理解呢,其实我也不太理解。。。
-
详细说明了分段的开销。

-
太好了,幸亏看了眼ppt发现不学非线性流水线的调度。
-
相关与冲突:相当恶心,邝坚的视频讲得还可以。
以及看完唯一的疑惑:

延迟分支就是为了保证分支指令之后能保证干一件有意义的事情,你再加个分支取消那和分支预测有啥区别?
仔细想了下好像明白了,延迟分支和预测分支是两个不同技术,之前有点把它们混为一谈了。单纯的延迟分支就是完全不预测,在分支出结果之前干点别的,分支取消算是两者的融合了,硬要说它比预测分支有什么好处的话,也许是可以随意根据可能性选择预测成功或失败,都可以有好处;而预测分支在教材中介绍的五段流水线中只有预测失败是有意义的,因为你预测成功也不能提前拿到跳转地址。
